La ley débil de los grandes números establece que si X1, X2, X3, ... es una sucesión infinita de variables aleatorias independientes que tienen el mismo valor esperado  y varianza
y varianza  , entonces el promedio:
, entonces el promedio:
 y varianza
y varianza  , entonces el promedio:
, entonces el promedio:
Converge en probabilidad a μ. En otras palabras, para cualquier número positivo ε se tiene:
La Ley Fuerte:
La ley fuerte de los grandes números establece que si X1, X2, X3, ... es una sucesión infinita de variables aleatorias independientes e idénticamente distribuidas que cumplen E(|Xi|) < ∞ y tienen el valor esperado μ, entonces:
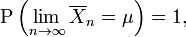
Es decir, el promedio de las variables aleatorias converge a μ casi seguramente (en un conjunto de probabilidad 1).
Esta ley justifica la interpretación intuitiva de que el valor esperado de una variable aleatoria como el "promedio a largo plazo al hacer un muestreo repetitivo".

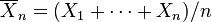

No hay comentarios:
Publicar un comentario
Nota: solo los miembros de este blog pueden publicar comentarios.