Jakob
Bernoulli (Basilea, 27 de diciembre de 1654 - ibíd. 16 de agosto de 1705),
también conocido como Jacob, Jacques o James Bernoulli, fue un genial
matemático y científico suizo y hermano mayor de Johann Bernoulli (parte de la
familia Bernoulli).
El primer libro sobre la teoría de la probabilidad fue Ars Conjectandi
de Jacques Bernoulli, publicado en 1713. En este libro se formula la Ley de los
Grandes Números: si un evento ocurre M veces sobre N intentos, al crecer el
número de intentos, la relación: (M/N) se acerca cada vez más a la probabilidad
del evento.
Siendo joven
su padre Nikolaus Bernoulli, lo envió a la Universidad de Basilea para estudiar
filosofía y teología, con el ánimo de que se convirtiera en teólogo. Pero Jakob
continuó, a escondidas, las que eran sus auténticas aficiones la física y las
matemáticas.
A partir de
los planteamientos de Leibniz desarrolló problemas de cálculo infinitesimal.
Fundó en Basilea un colegio experimental. Estudió por sí mismo la forma del
Cálculo ideada por Leibniz. Desde 1687 hasta su muerte fue profesor de
Matemáticas en Basilea. Jacob I fue uno de los primeros en desarrollar el
Cálculo más allá del estado en que lo dejaron Newton y Leibniz y en aplicarlo a
nuevos problemas difíciles e importantes. Sus contribuciones a la Geometría
analítica, a la teoría de probabilidades y al cálculo de variaciones, fueron de
extraordinaria importancia. Tenemos ya una muestra del tipo del problema
tratado por el cálculo de variaciones en el teorema de Fermat sobre el tiempo
mínimo. La matemática del problema se reduce a hacer que una cierta integral
tome un valor máximo sometido a una condición restrictiva. Jacob I resolvió
este problema y lo generalizó. el hecho de que la cicloide es la curva de más
rápido descenso fue descubierto por los hermanos Jacob I y Johannes I, en 1697,
y casi simultáneamente por varios autores Durante un viaje a Inglaterra en
1676, Jakob Bernoulli conoció a Robert Boyle yRobert Hooke. Este contacto le
inspiró una dedicación vitalicia a la ciencia y la matemática. Fue nombrado
Lector en la Universidad de Basilea en1682, y fue promocionado a Profesor de
Matemáticas en 1687.
En 1690 se
convirtió en la primera persona en desarrollar la técnica para resolver
ecuaciones diferenciales separables.
Se familiarizó
con el cálculo mediante su correspondencia con Gottfried Leibniz, y colaboró
con su hermano Johann en varias aplicaciones, siendo notable la publicación de
artículos en curvas trascendentales (1696) e isoperimetría (1700, 1701).
Su obra
maestra fue Ars Conjectandi (el Arte de la conjetura), un trabajo pionero en la
teoría de la probabilidad. La publicó su sobrino Nicholas en1713, ocho años
tras su muerte por tuberculosis. Los términos ensayo de Bernoulli y números de
Bernoulli son resultado de su trabajo. También existe un cráter en la Luna
bautizado cráter Bernoulli en honor suyo y de su hermano Johann.
es el error típico, o error estándar de la media.
se le denomina estimación puntual y se dice que 
se puede decir que 
es el error estándar estimado de la media,
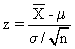
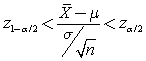
es la media (o la esperanza
matemática) y σ es la desviación típica, entonces podemos redefinir la relación
como:
.jpg){kind=small}